The Matrix class represents a transformation matrix that determines how to
map points from one coordinate space to another. You can perform various
graphical transformations on a display object by setting the properties of
a Matrix object, applying that Matrix object to the matrix property of a
Transform object, and then applying that Transform object as the
transform property of the display object. These transformation functions
include translation (x and y repositioning), rotation, scaling, and
skewing.
Together these types of transformations are known as affine
transformations. Affine transformations preserve the straightness of
lines while transforming, so that parallel lines stay parallel.
To apply a transformation matrix to a display object, you create a
Transform object, set its matrix property to the transformation matrix,
and then set the transform property of the display object to the
Transform object. Matrix objects are also used as parameters of some
methods, such as the following:
- The
draw()method of a BitmapData object - The
beginBitmapFill()method,beginGradientFill()method, orlineGradientStyle()method of a Graphics object
A transformation matrix object is a 3 x 3 matrix with the following contents:

In traditional transformation matrixes, the u, v, and w properties
provide extra capabilities. The Matrix class can only operate in
two-dimensional space, so it always assumes that the property values u
and v are 0.0, and that the property value w is 1.0. The effective
values of the matrix are as follows:

You can get and set the values of all six of the other properties in a
Matrix object: a, b, c, d, tx, and ty.
The Matrix class supports the four major types of transformations: translation, scaling, rotation, and skewing. You can set three of these transformations by using specialized methods, as described in the following table:
| Transformation | Method | Matrix values | Display result | Description |
|---|---|---|---|---|
| Translation (displacement) | translate(tx, ty) |  | 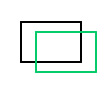 | Moves the image tx pixels to the right and ty pixels down. |
| Scaling | scale(sx, sy) |  | 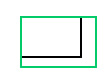 | Resizes the image, multiplying the location of each pixel by sx on the x axis and sy on the y axis. |
| Rotation | rotate(q) | 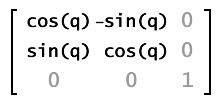 | 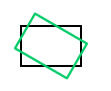 | Rotates the image by an angle q, which is measured in radians. |
| Skewing or shearing | None; must set the properties b and c | 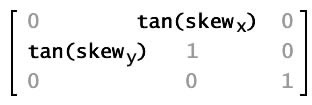 | 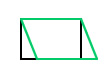 | Progressively slides the image in a direction parallel to the x or y axis. The b property of the Matrix object represents the tangent of the skew angle along the y axis; the c property of the Matrix object represents the tangent of the skew angle along the x axis. |
Each transformation function alters the current matrix properties so that
you can effectively combine multiple transformations. To do this, you call
more than one transformation function before applying the matrix to its
display object target (by using the transform property of that display
object).
Use the new Matrix() constructor to create a Matrix object before you
can call the methods of the Matrix object.
See also:
Constructor
new(a:Float = 1, b:Float = 0, c:Float = 0, d:Float = 1, tx:Float = 0, ty:Float = 0)
Creates a new Matrix object with the specified parameters. In matrix notation, the properties are organized like this:

If you do not provide any parameters to the new Matrix()
constructor, it creates an identity matrix with the following
values:
a = 1 | b = 0 |
|---|---|
tx = 0 | ty = 0 |
In matrix notation, the identity matrix looks like this:

Parameters:
a | The value that affects the positioning of pixels along the x axis when scaling or rotating an image. |
|---|---|
b | The value that affects the positioning of pixels along the y axis when rotating or skewing an image. |
c | The value that affects the positioning of pixels along the x axis when rotating or skewing an image. |
d | The value that affects the positioning of pixels along the y axis when scaling or rotating an image.. |
tx | The distance by which to translate each point along the x axis. |
ty | The distance by which to translate each point along the y axis. |
Variables
a:Float
The value that affects the positioning of pixels along the x axis when scaling or rotating an image.
b:Float
The value that affects the positioning of pixels along the y axis when rotating or skewing an image.
c:Float
The value that affects the positioning of pixels along the x axis when rotating or skewing an image.
d:Float
The value that affects the positioning of pixels along the y axis when scaling or rotating an image.
Methods
clone():Matrix
Returns a new Matrix object that is a clone of this matrix, with an exact copy of the contained object.
Returns:
A Matrix object.
concat(m:Matrix):Void
Concatenates a matrix with the current matrix, effectively combining the geometric effects of the two. In mathematical terms, concatenating two matrixes is the same as combining them using matrix multiplication.
For example, if matrix m1 scales an object by a factor of
four, and matrix m2 rotates an object by 1.5707963267949
radians(Math.PI/2), then m1.concat(m2)
transforms m1 into a matrix that scales an object by a factor
of four and rotates the object by Math.PI/2 radians.
This method replaces the source matrix with the concatenated matrix. If
you want to concatenate two matrixes without altering either of the two
source matrixes, first copy the source matrix by using the
clone() method, as shown in the Class Examples section.
Parameters:
m | The matrix to be concatenated to the source matrix. |
|---|
copyColumnFrom(column:Int, vector3D:Vector3D):Void
Copies a Vector3D object into specific column of the calling Matrix3D object.
Parameters:
column | The column from which to copy the data from. |
|---|---|
vector3D | The Vector3D object from which to copy the data. |
copyColumnTo(column:Int, vector3D:Vector3D):Void
Copies specific column of the calling Matrix object into the Vector3D object. The
w element of the Vector3D object will not be changed.
Parameters:
column | The column from which to copy the data from. |
|---|---|
vector3D | The Vector3D object from which to copy the data. |
copyFrom(sourceMatrix:Matrix):Void
Copies all of the matrix data from the source Point object into the calling Matrix object.
Parameters:
sourceMatrix | The Matrix object from which to copy the data. |
|---|
copyRowFrom(row:Int, vector3D:Vector3D):Void
Copies a Vector3D object into specific row of the calling Matrix object.
Parameters:
row | The row from which to copy the data from. |
|---|---|
vector3D | The Vector3D object from which to copy the data. |
copyRowTo(row:Int, vector3D:Vector3D):Void
Copies specific row of the calling Matrix object into the Vector3D object. The w
element of the Vector3D object will not be changed.
Parameters:
row | The row from which to copy the data from. |
|---|---|
vector3D | The Vector3D object from which to copy the data. |
createBox(scaleX:Float, scaleY:Float, rotation:Float = 0, tx:Float = 0, ty:Float = 0):Void
Includes parameters for scaling, rotation, and translation. When
applied to a matrix it sets the matrix's values based on those
parameters.
Using the createBox() method lets you obtain the same matrix as you
would if you applied the identity(), rotate(), scale(), and
translate() methods in succession. For example,
mat1.createBox(2,2,Math.PI/4, 100, 100) has the same effect as the
following:
import openfl.geom.Matrix;
var mat1 = new Matrix();
mat1.identity();
mat1.rotate(Math.PI/4);
mat1.scale(2,2);
mat1.translate(10,20);Parameters:
scaleX | The factor by which to scale horizontally. |
|---|---|
scaleY | The factor by which scale vertically. |
rotation | The amount to rotate, in radians. |
tx | The number of pixels to translate (move) to the right along the x axis. |
ty | The number of pixels to translate (move) down along the y axis. |
createGradientBox(width:Float, height:Float, rotation:Float = 0, tx:Float = 0, ty:Float = 0):Void
Creates the specific style of matrix expected by the
beginGradientFill() and lineGradientStyle() methods of the
Graphics class. Width and height are scaled to a scaleX/scaleY
pair and the tx/ty values are offset by half the width and height.
For example, consider a gradient with the following characteristics:
GradientType.LINEAR- Two colors, green and blue, with the ratios array set to
[0, 255] SpreadMethod.PADInterpolationMethod.LINEAR_RGB
The following illustrations show gradients in which the matrix was
defined using the createGradientBox() method with different
parameter settings:
createGradientBox() settings | Resulting gradient |
|---|---|
width = 25; height = 25; rotation = 0; tx = 0; ty = 0; |  |
width = 25; height = 25; rotation = 0; tx = 25; ty = 0; |  |
width = 50; height = 50; rotation = 0; tx = 0; ty = 0; |  |
width = 50; height = 50; rotation = Math.PI / 4; // 45 degrees tx = 0; ty = 0; |  |
Parameters:
width | The width of the gradient box. |
|---|---|
height | The height of the gradient box. |
rotation | The amount to rotate, in radians. |
tx | The distance, in pixels, to translate to the right
along the x axis. This value is offset by half of
the |
ty | The distance, in pixels, to translate down along the
y axis. This value is offset by half of the |
deltaTransformPoint(point:Point):Point
Given a point in the pretransform coordinate space, returns the
coordinates of that point after the transformation occurs. Unlike the
standard transformation applied using the transformPoint()
method, the deltaTransformPoint() method's transformation
does not consider the translation parameters tx and
ty.
Parameters:
point | The point for which you want to get the result of the matrix transformation. |
|---|
Returns:
The point resulting from applying the matrix transformation.
deltaTransformPointToOutput(point:Point, output:Point):Point
Given a point in the pretransform coordinate space, returns the
coordinates of that point after the transformation occurs. Unlike the
standard transformation applied using the transformPoint()
method, the deltaTransformPoint() method's transformation
does not consider the translation parameters tx and
ty.
Parameters:
point | The point for which you want to get the result of the matrix transformation. |
|---|---|
output | An optional point to be set with the output value and returned, to avoid the runtime creating a new point object. |
Returns:
The point resulting from applying the matrix transformation.
identity():Void
Sets each matrix property to a value that causes a null
transformation. An object transformed by applying an identity matrix
will be identical to the original.
After calling the identity() method, the resulting matrix has the
following properties: a=1, b=0, c=0, d=1, tx=0, ty=0.
In matrix notation, the identity matrix looks like this:

invert():Matrix
Performs the opposite transformation of the original matrix. You can apply an inverted matrix to an object to undo the transformation performed when applying the original matrix.
rotate(theta:Float):Void
Applies a rotation transformation to the Matrix object.
The rotate() method alters the a, b, c, and d properties of
the Matrix object. In matrix notation, this is the same as
concatenating the current matrix with the following:
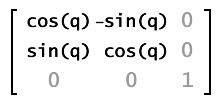
Parameters:
angle | The rotation angle in radians. |
|---|
scale(sx:Float, sy:Float):Void
Applies a scaling transformation to the matrix. The x axis is
multiplied by sx, and the y axis it is multiplied by sy.
The scale() method alters the a and d properties of the Matrix
object. In matrix notation, this is the same as concatenating the
current matrix with the following matrix:

Parameters:
sx | A multiplier used to scale the object along the x axis. |
|---|---|
sy | A multiplier used to scale the object along the y axis. |
setTo(a:Float, b:Float, c:Float, d:Float, tx:Float, ty:Float):Void
Sets the members of Matrix to the specified values
Parameters:
aa | the values to set the matrix to. |
|---|---|
ba | |
ca | |
da | |
txa | |
null | tya |
toString():String
Returns a text value listing the properties of the Matrix object.
Returns:
A string containing the values of the properties of the Matrix
object: a, b, c,
d, tx, and ty.
transformPoint(pos:Point):Point
Returns the result of applying the geometric transformation represented by the Matrix object to the specified point.
Parameters:
point | The point for which you want to get the result of the Matrix transformation. |
|---|
Returns:
The point resulting from applying the Matrix transformation.
transformPointToOutput(pos:Point, output:Point):Point
Returns the result of applying the geometric transformation represented by the Matrix object to the specified point.
Parameters:
point | The point for which you want to get the result of the Matrix transformation. |
|---|---|
output | An optional point to be set with the output value and returned, to avoid the runtime creating a new point object. |
Returns:
The point resulting from applying the Matrix transformation.
translate(dx:Float, dy:Float):Void
Translates the matrix along the x and y axes, as specified
by the dx and dy parameters.
Parameters:
dx | The amount of movement along the x axis to the right, in pixels. |
|---|---|
dy | The amount of movement down along the y axis, in pixels. |