The Vector3D class represents a point or a location in the three-dimensional space using
the Cartesian coordinates x, y, and z. As in a two-dimensional space, the x property
represents the horizontal axis and the y property represents the vertical axis. In
three-dimensional space, the z property represents depth. The value of the x property increases as the object moves to the right. The value of the y property
increases as the object moves down. The z property increases as the object moves
farther from the point of view. Using perspective projection and scaling, the object is
seen to be bigger when near and smaller when farther away from the screen. As in a
right-handed three-dimensional coordinate system, the positive z-axis points away from
the viewer and the value of the z property increases as the object moves away from the
viewer's eye. The origin point (0,0,0) of the global space is the upper-left corner of
the stage.
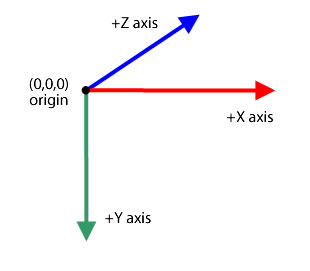
The Vector3D class can also represent a direction, an arrow pointing from the origin of the coordinates, such as (0,0,0), to an endpoint; or a floating-point component of an RGB (Red, Green, Blue) color model.
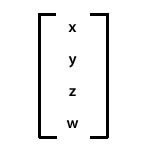
Quaternion notation introduces a fourth element, the w property, which provides
additional orientation information. For example, the w property can define an angle
of rotation of a Vector3D object. The combination of the angle of rotation and the
coordinates x, y, and z can determine the display object's orientation. Here is
a representation of Vector3D elements in matrix notation:
Static variables
Static methods
staticangleBetween(a:Vector3D, b:Vector3D):Float
Returns the angle in radians between two vectors. The returned angle is the smallest radian the first Vector3D object rotates until it aligns with the second Vector3D object.
The angleBetween() method is a static method. You can use it directly as a method
of the Vector3D class.
To convert a degree to a radian, you can use the following formula:
radian = Math.PI/180 * degreeParameters:
a | The first Vector3D object. |
|---|---|
b | The second Vector3D object. |
Returns:
The angle between two Vector3D objects.
staticdistance(pt1:Vector3D, pt2:Vector3D):Float
Returns the distance between two Vector3D objects. The distance() method is a
static method. You can use it directly as a method of the Vector3D class to get
the Euclidean distance between two three-dimensional points.
Parameters:
pt1 | A Vector3D object as the first three-dimensional point. |
|---|---|
pt2 | A Vector3D object as the second three-dimensional point. |
Returns:
The distance between two Vector3D objects.
Constructor
new(x:Float = 0, y:Float = 0, z:Float = 0, w:Float = 0)
Creates an instance of a Vector3D object. If you do not specify a parameter for the constructor, a Vector3D object is created with the elements (0,0,0,0).
Parameters:
x | The first element, such as the x coordinate. |
|---|---|
y | The second element, such as the y coordinate. |
z | The third element, such as the z coordinate. |
w | An optional element for additional data such as the angle of rotation. |
Variables
read onlylength:Float
The length, magnitude, of the current Vector3D object from the origin (0,0,0) to
the object's x, y, and z coordinates. The w property is ignored. A unit vector has
a length or magnitude of one.
read onlylengthSquared:Float
The square of the length of the current Vector3D object, calculated using the x,
y, and z properties. The w property is ignored. Use the lengthSquared()
method whenever possible instead of the slower Math.sqrt() method call of the
Vector3D.length() method.
w:Float
The fourth element of a Vector3D object (in addition to the x, y, and z
properties) can hold data such as the angle of rotation. The default value is 0.
Quaternion notation employs an angle as the fourth element in its calculation of three-dimensional rotation. The w property can be used to define the angle of rotation about the Vector3D object. The combination of the rotation angle and the coordinates (x,y,z) determines the display object's orientation.
In addition, the w property can be used as a perspective warp factor for a
projected three-dimensional position or as a projection transform value in
representing a three-dimensional coordinate projected into the two-dimensional
space. For example, you can create a projection matrix using the Matrix3D.rawData
property, that, when applied to a Vector3D object, produces a transform value in
the Vector3D object's fourth element (the w property). Dividing the Vector3D
object's other elements by the transform value then produces a projected Vector3D
object. You can use the Vector3D.project() method to divide the first three
elements of a Vector3D object by its fourth element.
x:Float
The first element of a Vector3D object, such as the x coordinate of a point in the three-dimensional space. The default value is 0.
y:Float
The second element of a Vector3D object, such as the y coordinate of a point in the three-dimensional space. The default value is 0.
z:Float
The third element of a Vector3D object, such as the z coordinate of a point in three-dimensional space. The default value is 0.
Methods
add(a:Vector3D):Vector3D
Adds the value of the x, y, and z elements of the current Vector3D object to the
values of the x, y, and z elements of another Vector3D object. The add() method
does not change the current Vector3D object. Instead, it returns a new Vector3D
object with the new values.
The result of adding two vectors together is a resultant vector. One way to visualize the result is by drawing a vector from the origin or tail of the first vector to the end or head of the second vector. The resultant vector is the distance between the origin point of the first vector and the end point of the second vector.
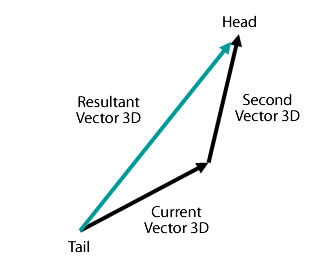
Parameters:
a | A Vector3D object to be added to the current Vector3D object. |
|---|
Returns:
A Vector3D object that is the result of adding the current Vector3D object to another Vector3D object.
addToOutput(a:Vector3D, output:Vector3D):Vector3D
Adds the value of the x, y, and z elements of the current Vector3D object to the
values of the x, y, and z elements of another Vector3D object. The add() method
does not change the current Vector3D object. Instead, it returns a new Vector3D
object with the new values.
The result of adding two vectors together is a resultant vector. One way to visualize the result is by drawing a vector from the origin or tail of the first vector to the end or head of the second vector. The resultant vector is the distance between the origin point of the first vector and the end point of the second vector.

Parameters:
a | A Vector3D object to be added to the current Vector3D object. |
|---|---|
output | An optional Vector3D object to be used as the output value, avoiding the creation of a new object |
Returns:
A Vector3D object that is the result of adding the current Vector3D object to another Vector3D object.
clone():Vector3D
Returns a new Vector3D object that is an exact copy of the current Vector3D object.
Returns:
A new Vector3D object that is a copy of the current Vector3D object.
copyFrom(sourceVector3D:Vector3D):Void
Copies all of vector data from the source Vector3D object into the calling Vector3D object.
Parameters:
sourceVector3D | The Vector3D object from which to copy the data. |
|---|
crossProduct(a:Vector3D):Vector3D
Returns a new Vector3D object that is perpendicular (at a right angle) to the current Vector3D and another Vector3D object. If the returned Vector3D object's coordinates are (0,0,0), then the two Vector3D objects are parallel to each other.
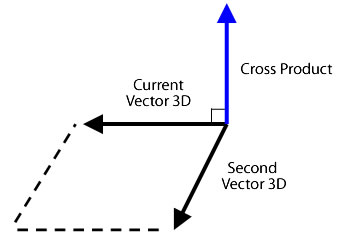
You can use the normalized cross product of two vertices of a polygon surface with the normalized vector of the camera or eye viewpoint to get a dot product. The value of the dot product can identify whether a surface of a three-dimensional object is hidden from the viewpoint.
Parameters:
a | A second Vector3D object. |
|---|
Returns:
A new Vector3D object that is perpendicular to the current Vector3D object and the Vector3D object specified as the parameter.
crossProductToOutput(a:Vector3D, output:Vector3D):Vector3D
Returns a new Vector3D object that is perpendicular (at a right angle) to the current Vector3D and another Vector3D object. If the returned Vector3D object's coordinates are (0,0,0), then the two Vector3D objects are parallel to each other.

You can use the normalized cross product of two vertices of a polygon surface with the normalized vector of the camera or eye viewpoint to get a dot product. The value of the dot product can identify whether a surface of a three-dimensional object is hidden from the viewpoint.
Parameters:
a | A second Vector3D object. |
|---|---|
output | An optional Vector3D object to be used as the output value, avoiding the creation of a new object |
Returns:
A new Vector3D object that is perpendicular to the current Vector3D object and the Vector3D object specified as the parameter.
decrementBy(a:Vector3D):Void
Decrements the value of the x, y, and z elements of the current Vector3D object by
the values of the x, y, and z elements of specified Vector3D object. Unlike the
Vector3D.subtract() method, the decrementBy() method changes the current
Vector3D object and does not return a new Vector3D object.
Parameters:
a | The Vector3D object containing the values to subtract from the current Vector3D object. |
|---|
dotProduct(a:Vector3D):Float
If the current Vector3D object and the one specified as the parameter are unit
vertices, this method returns the cosine of the angle between the two vertices.
Unit vertices are vertices that point to the same direction but their length is
one. They remove the length of the vector as a factor in the result. You can use
the normalize() method to convert a vector to a unit vector.
The dotProduct() method finds the angle between two vertices. It is also used in
backface culling or lighting calculations. Backface culling is a procedure for
determining which surfaces are hidden from the viewpoint. You can use the
normalized vertices from the camera, or eye, viewpoint and the cross product of
the vertices of a polygon surface to get the dot product. If the dot product is less
than zero, then the surface is facing the camera or the viewer. If the two unit
vertices are perpendicular to each other, they are orthogonal and the dot product
is zero. If the two vertices are parallel to each other, the dot product is one.
Parameters:
a | The second Vector3D object. |
|---|
Returns:
A scalar which is the dot product of the current Vector3D object and the specified Vector3D object.
equals(toCompare:Vector3D, allFour:Bool = false):Bool
Determines whether two Vector3D objects are equal by comparing the x, y, and z
elements of the current Vector3D object with a specified Vector3D object. If the
values of these elements are the same, the two Vector3D objects are equal. If the
second optional parameter is set to true, all four elements of the Vector3D
objects, including the w property, are compared.
Parameters:
toCompare | The Vector3D object to be compared with the current Vector3D object. |
|---|---|
allFour | An optional parameter that specifies whether the |
Returns:
A value of true if the specified Vector3D object is equal to the current Vector3D object; false if it is not equal.
incrementBy(a:Vector3D):Void
Increments the value of the x, y, and z elements of the current Vector3D object by
the values of the x, y, and z elements of a specified Vector3D object. Unlike the
Vector3D.add() method, the incrementBy() method changes the current Vector3D
object and does not return a new Vector3D object.
Parameters:
a | The Vector3D object to be added to the current Vector3D object. |
|---|
nearEquals(toCompare:Vector3D, tolerance:Float, allFour:Bool = false):Bool
Compares the elements of the current Vector3D object with the elements of a specified Vector3D object to determine whether they are nearly equal. The two Vector3D objects are nearly equal if the value of all the elements of the two vertices are equal, or the result of the comparison is within the tolerance range. The difference between two elements must be less than the number specified as the tolerance parameter. If the third optional parameter is set to true, all four elements of the Vector3D objects, including the w property, are compared. Otherwise, only the x, y, and z elements are included in the comparison.
Parameters:
toCompare | The Vector3D object to be compared with the current Vector3D object. |
|---|---|
tolerance | A number determining the tolerance factor. If the difference between the values of the Vector3D element specified in the toCompare parameter and the current Vector3D element is less than the tolerance number, the two values are considered nearly equal. |
allFour | An optional parameter that specifies whether the |
Returns:
A value of true if the specified Vector3D object is nearly equal to the current Vector3D object; false if it is not equal.
negate():Void
Sets the current Vector3D object to its inverse. The inverse object is also
considered the opposite of the original object. The value of the x, y, and z
properties of the current Vector3D object is changed to -x, -y, and -z.
normalize():Float
Converts a Vector3D object to a unit vector by dividing the first three elements
(x, y, z) by the length of the vector. Unit vertices are vertices that have a
direction but their length is one. They simplify vector calculations by removing length as a factor.
Returns:
The length of the current Vector3D object.
project():Void
Divides the value of the x, y, and z properties of the current Vector3D
object by the value of its w property.
If the current Vector3D object is the result of multiplying a Vector3D object by a
projection Matrix3D object, the w property can hold the transform value. The
project() method then can complete the projection by dividing the elements by the
w property. Use the Matrix3D.rawData property to create a projection Matrix3D
object.
scaleBy(s:Float):Void
Scales the current Vector3D object by a scalar, a magnitude. The Vector3D object's x, y, and z elements are multiplied by the scalar number specified in the parameter. For example, if the vector is scaled by ten, the result is a vector that is ten times longer. The scalar can also change the direction of the vector. Multiplying the vector by a negative number reverses its direction.
Parameters:
s | A multiplier (scalar) used to scale a Vector3D object. |
|---|
setTo(xa:Float, ya:Float, za:Float):Void
Sets the members of Vector3D to the specified values
Parameters:
xa | the values to set the vector to. |
|---|---|
ya | |
null | za |
subtract(a:Vector3D):Vector3D
Subtracts the value of the x, y, and z elements of the current Vector3D object
from the values of the x, y, and z elements of another Vector3D object. The
subtract() method does not change the current Vector3D object. Instead, this
method returns a new Vector3D object with the new values.
Parameters:
a | The Vector3D object to be subtracted from the current Vector3D object. |
|---|
Returns:
A new Vector3D object that is the difference between the current Vector3D and the specified Vector3D object.
subtractToOutput(a:Vector3D, output:Vector3D):Vector3D
Subtracts the value of the x, y, and z elements of the current Vector3D object
from the values of the x, y, and z elements of another Vector3D object. The
subtract() method does not change the current Vector3D object. Instead, this
method returns a new Vector3D object with the new values.
Parameters:
a | The Vector3D object to be subtracted from the current Vector3D object. |
|---|---|
output | An optional Vector3D object to be used as the output value, avoiding the creation of a new object |
Returns:
A new Vector3D object that is the difference between the current Vector3D and the specified Vector3D object.
toString():String
Returns a string representation of the current Vector3D object. The string contains the values of the x, y, and z properties.
Returns:
A string containing the values of the x, y, and z properties.