class Matrix3D
package openfl.geom
extended by PerspectiveMatrix3D
Available on all platforms
The Matrix3D class represents a transformation matrix that determines the position and orientation of a three-dimensional (3D) display object. The matrix can perform transformation functions including translation (repositioning along the x, y, and z axes), rotation, and scaling (resizing). The Matrix3D class can also perform perspective projection, which maps points from the 3D coordinate space to a two-dimensional (2D) view.
A single matrix can combine multiple transformations and apply them at once to a 3D display object. For example, a matrix can be applied to 3D coordinates to perform a rotation followed by a translation.
When you explicitly set the z property or any of the rotation or scaling properties
of a display object, a corresponding Matrix3D object is automatically created.
You can access a 3D display object's Matrix3D object through the transform.matrix3d
property. 2D objects do not have a Matrix3D object.
The value of the z property of a 2D object is zero and the value of its matrix3D
property is null.
Note: If the same Matrix3D object is assigned to two different display objects, a runtime error is thrown.
The Matrix3D class uses a 4x4 square matrix: a table of four rows and columns of numbers that hold the data for the transformation. The first three rows of the matrix hold data for each 3D axis (x,y,z). The translation information is in the last column. The orientation and scaling data are in the first three columns. The scaling factors are the diagonal numbers in the first three columns. Here is a representation of Matrix3D elements:
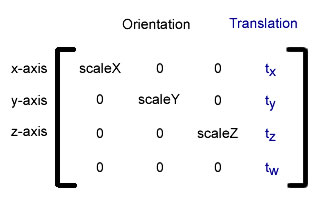
You don't need to understand matrix mathematics to use the Matrix3D class. It offers
specific methods that simplify the task of transformation and projection, such as the
appendTranslation(), appendRotation(), or interpolateTo() methods. You also can
use the decompose() and recompose() methods or the rawData property to access
the underlying matrix elements.
Display objects cache their axis rotation properties to have separate rotation for each axis and to manage the different combinations of rotations. When a method of a Matrix3D object is called to transform a display object, the rotation cache of the object is invalidated.
Static methods
staticinterpolate(thisMat:Matrix3D, toMat:Matrix3D, percent:Float):Matrix3D
Interpolates the translation, rotation, and scale transformation of one matrix toward those of the target matrix.
The interpolate() method avoids some of the unwanted results that can occur
when using methods such as the display object's axis rotation properties. The
interpolate() method invalidates the cached value of the rotation property of
the display object and converts the orientation elements of the display object's
matrix to a quaternion before interpolation. This method guarantees the shortest,
most efficient path for the rotation. It also produces a smooth, gimbal-lock-free
rotation. A gimbal lock can occur when using Euler Angles, where each axis is
handled independently. During the rotation around two or more axes, the axes can
become aligned, leading to unexpected results. Quaternion rotation avoids the
gimbal lock.
Consecutive calls to the interpolate() method can produce the effect of a
display object starting quickly and then slowly approaching another display
object. For example, if you set the thisMat parameter to the returned Matrix3D
object, the toMat parameter to the target display object's associated Matrix3D
object, and the percent parameter to 0.1, the display object moves ten percent
toward the target object. On subsequent calls or in subsequent frames, the object
moves ten percent of the remaining 90 percent, then ten percent of the remaining
distance, and continues until it reaches the target.
Parameters:
thisMat | The Matrix3D object that is to be interpolated. |
|---|---|
toMat | The target Matrix3D object. |
percent | A value between 0 and 1 that determines the percent the
|
Returns:
A Matrix3D object with elements that place the values of the matrix between the original matrix and the target matrix. When the returned matrix is applied to the this display object, the object moves the specified percent closer to the target object.
staticinterpolateToOutput(thisMat:Matrix3D, toMat:Matrix3D, percent:Float, output:Matrix3D):Matrix3D
Interpolates the translation, rotation, and scale transformation of one matrix toward those of the target matrix.
The interpolate() method avoids some of the unwanted results that can occur
when using methods such as the display object's axis rotation properties. The
interpolate() method invalidates the cached value of the rotation property of
the display object and converts the orientation elements of the display object's
matrix to a quaternion before interpolation. This method guarantees the shortest,
most efficient path for the rotation. It also produces a smooth, gimbal-lock-free
rotation. A gimbal lock can occur when using Euler Angles, where each axis is
handled independently. During the rotation around two or more axes, the axes can
become aligned, leading to unexpected results. Quaternion rotation avoids the
gimbal lock.
Consecutive calls to the interpolate() method can produce the effect of a
display object starting quickly and then slowly approaching another display
object. For example, if you set the thisMat parameter to the returned Matrix3D
object, the toMat parameter to the target display object's associated Matrix3D
object, and the percent parameter to 0.1, the display object moves ten percent
toward the target object. On subsequent calls or in subsequent frames, the object
moves ten percent of the remaining 90 percent, then ten percent of the remaining
distance, and continues until it reaches the target.
Parameters:
thisMat | The Matrix3D object that is to be interpolated. |
|---|---|
toMat | The target Matrix3D object. |
percent | A value between 0 and 1 that determines the percent the
|
output | An optional Matrix3D object to be used and returned to avoid the runtime creating a new object. |
Returns:
A Matrix3D object with elements that place the values of the matrix between the original matrix and the target matrix. When the returned matrix is applied to the this display object, the object moves the specified percent closer to the target object.
Constructor
Variables
read onlydeterminant:Float
A Number that determines whether a matrix is invertible.
A Matrix3D object must be invertible. You can use the determinant property to make
sure that a Matrix3D object is invertible. If determinant is zero, an inverse of
the matrix does not exist. For example, if an entire row or column of a matrix is
zero or if two rows or columns are equal, the determinant is zero. Determinant is
also used to solve a series of equations.
Only a square matrix, like the Matrix3D class, has a determinant.
position:Vector3D
A Vector3D object that holds the position, the 3D coordinate (x,y,z) of a display
object within the transformation's frame of reference. The position property
provides immediate access to the translation vector of the display object's
matrix without needing to decompose and recompose the matrix.
With the position property, you can get and set the translation elements of the
transformation matrix.
rawData:Vector<Float>
A Vector of 16 Numbers, where every four elements is a column of a 4x4 matrix.
An exception is thrown if the rawData property is set to a matrix that is not
invertible. The Matrix3D object must be invertible. If a non-invertible matrix is
needed, create a subclass of the Matrix3D object.
Methods
append(lhs:Matrix3D):Void
A Vector of 16 Numbers, where every four elements is a column of a 4x4 matrix.
An exception is thrown if the rawData property is set to a matrix that is not
invertible. The Matrix3D object must be invertible. If a non-invertible matrix is
needed, create a subclass of the Matrix3D object.
appendRotation(degrees:Float, axis:Vector3D, ?pivotPoint:Vector3D):Void
Appends an incremental rotation to a Matrix3D object. When the Matrix3D object is applied to a display object, the matrix performs the rotation after other transformations in the Matrix3D object.
The display object's rotation is defined by an axis, an incremental degree of
rotation around the axis, and an optional pivot point for the center of the
object's rotation. The axis can be any general direction. The common axes are the
X_AXIS (Vector3D(1,0,0)), Y_AXIS (Vector3D(0,1,0)), and
Z_AXIS (Vector3D(0,0,1)). In aviation terminology, the rotation about the y axis
is called yaw. The rotation about the x axis is called pitch. The rotation about
the z axis is called roll.
The order of transformation matters. A rotation followed by a translation transformation produces a different effect than a translation followed by a rotation transformation.
The rotation effect is not absolute. It is relative to the current position and
orientation. To make an absolute change to the transformation matrix, use the
recompose() method. The appendRotation() method is also different from the
axis rotation property of the display object, such as rotationX property. The
rotation property is always performed before any translation, whereas the
appendRotation() method is performed relative to what is already in the matrix.
To make sure that you get a similar effect as the display object's axis rotation
property, use the prependRotation() method, which performs the rotation before
other transformations in the matrix.
When the appendRotation() method's transformation is applied to a Matrix3D object
of a display object, the cached rotation property values of the display object
are invalidated.
One way to have a display object rotate around a specific point relative to its
location is to set the translation of the object to the specified point, rotate
the object using the appendRotation() method, and translate the object back to
the original position. In the following example, the myObject 3D display object
makes a y-axis rotation around the coordinate (10,10,0).
myObject.z = 1;
myObject.transform.matrix3D.appendTranslation(10,10,0);
myObject.transform.matrix3D.appendRotation(1, Vector3D.Y_AXIS);
myObject.transform.matrix3D.appendTranslation(-10,-10,0);Parameters:
degrees | The degree of the rotation. |
|---|---|
axis | The axis or direction of rotation. The usual axes are the
|
pivotPoint | A point that determines the center of an object's rotation. The default pivot point for an object is its registration point. |
appendScale(xScale:Float, yScale:Float, zScale:Float):Void
Appends an incremental scale change along the x, y, and z axes to a Matrix3D object. When the Matrix3D object is applied to a display object, the matrix performs the scale changes after other transformations in the Matrix3D object. The default scale factor is (1.0, 1.0, 1.0).
The scale is defined as a set of three incremental changes along the three axes (x,y,z). You can multiply each axis with a different number. When the scale changes are applied to a display object, the object's size increases or decreases. For example, setting the x, y, and z axes to two doubles the size of the object, while setting the axes to 0.5 halves the size. To make sure that the scale transformation only affects a specific axis, set the other parameters to one. A parameter of one means no scale change along the specific axis.
The appendScale() method can be used for resizing as well as for managing
distortions, such as stretch or contract of a display object, or for zooming in
and out on a location. Scale transformations are automatically performed during a
display object's rotation and translation.
The order of transformation matters. A resizing followed by a translation transformation produces a different effect than a translation followed by a resizing transformation.
Parameters:
xScale | A multiplier used to scale the object along the x axis. |
|---|---|
yScale | A multiplier used to scale the object along the y axis. |
zScale | A multiplier used to scale the object along the z axis. |
appendTranslation(x:Float, y:Float, z:Float):Void
Appends an incremental translation, a repositioning along the x, y, and z axes, to a Matrix3D object. When the Matrix3D object is applied to a display object, the matrix performs the translation changes after other transformations in the Matrix3D object.
The translation is defined as a set of three incremental changes along the three axes (x,y,z). When the transformation is applied to a display object, the display object moves from it current location along the x, y, and z axes as specified by the parameters. To make sure that the translation only affects a specific axis, set the other parameters to zero. A zero parameter means no change along the specific axis.
The translation changes are not absolute. They are relative to the current position and orientation of the matrix. To make an absolute change to the transformation matrix, use the recompose() method. The order of transformation also matters. A translation followed by a rotation transformation produces a different effect than a rotation followed by a translation.
Parameters:
x | An incremental translation along the x axis. |
|---|---|
y | An incremental translation along the y axis. |
z | An incremental translation along the z axis. |
clone():Matrix3D
Returns a new Matrix3D object that is an exact copy of the current Matrix3D object.
Returns:
A new Matrix3D object that is an exact copy of the current Matrix3D object.
copyColumnFrom(column:Int, vector3D:Vector3D):Void
Copies a Vector3D object into specific column of the calling Matrix3D object.
Parameters:
column | The destination column of the copy. |
|---|---|
vector3D | The Vector3D object from which to copy the data. |
copyColumnTo(column:Int, vector3D:Vector3D):Void
Copies specific column of the calling Matrix3D object into the Vector3D object.
Parameters:
column | The column from which to copy the data. |
|---|---|
vector3D | The destination Vector3D object of the copy. |
copyFrom(other:Matrix3D):Void
Copies all of the matrix data from the source Matrix3D object into the calling Matrix3D object.
Parameters:
sourceMatrix3D | The Matrix3D object from which to copy the data. |
|---|
copyRawDataFrom(vector:Vector<Float>, index:UInt = 0, transpose:Bool = false):Void
Copies all of the vector data from the source vector object into the calling
Matrix3D object. The optional index parameter allows you to select any starting
slot in the vector.
Parameters:
vector | The vector object from which to copy the data. |
|---|---|
index | |
null | transpose |
copyRawDataTo(vector:Vector<Float>, index:UInt = 0, transpose:Bool = false):Void
Copies all of the matrix data from the calling Matrix3D object into the provided vector. The optional index parameter allows you to select any target starting slot in the vector.
Parameters:
vector | The vector object to which to copy the data. |
|---|---|
index | |
null | transpose |
copyRowFrom(row:UInt, vector3D:Vector3D):Void
Copies a Vector3D object into specific row of the calling Matrix3D object.
Parameters:
row | The row from which to copy the data to. |
|---|---|
vector3D | The Vector3D object from which to copy the data. |
copyRowTo(row:Int, vector3D:Vector3D):Void
Copies specific row of the calling Matrix3D object into the Vector3D object.
Parameters:
row | The row from which to copy the data from. |
|---|---|
vector3D | The Vector3D object to copy the data into. |
decompose(orientationStyle:Orientation3D = EULER_ANGLES):Vector<Vector3D>
Returns the transformation matrix's translation, rotation, and scale settings as a Vector of three Vector3D objects. The first Vector3D object holds the translation elements. The second Vector3D object holds the rotation elements. The third Vector3D object holds the scale elements.
Some Matrix3D methods, such as the interpolateTo() method, automatically
decompose and recompose the matrix to perform their transformation.
To modify the matrix's transformation with an absolute parent frame of reference,
retrieve the settings with the decompose() method and make the appropriate
changes. You can then set the Matrix3D object to the modified transformation
using the recompose() method.
The decompose() method's parameter specifies the orientation style that is
meant to be used for the transformation. The default orientation is eulerAngles,
which defines the orientation with three separate angles of rotation for each
axis. The rotations occur consecutively and do not change the axis of each other.
The display object's axis rotation properties perform Euler Angles orientation
style transformation. The other orientation style options are axisAngle and
quaternion. The Axis Angle orientation uses a combination of an axis and an
angle to determine the orientation. The axis around which the object is rotated
is a unit vector that represents a direction. The angle represents the magnitude
of the rotation about the vector. The direction also determines where a display
object is facing and the angle determines which way is up. The appendRotation()
and prependRotation() methods use the Axis Angle orientation. The quaternion
orientation uses complex numbers and the fourth element of a vector. The three
axes of rotation (x,y,z) and an angle of rotation (w) represent the orientation.
The interpolate() method uses quaternion.
Parameters:
orientationStyle | An optional parameter that determines the orientation
style used for the matrix transformation. The three types of orientation style
are |
|---|
Returns:
A Vector of three Vector3D objects, each holding the translation, rotation, and scale settings, respectively.
decomposeToOutput(orientationStyle:Orientation3D = EULER_ANGLES, ?output:Vector<Vector3D>):Vector<Vector3D>
Returns the transformation matrix's translation, rotation, and scale settings as a Vector of three Vector3D objects. The first Vector3D object holds the translation elements. The second Vector3D object holds the rotation elements. The third Vector3D object holds the scale elements.
Some Matrix3D methods, such as the interpolateTo() method, automatically
decompose and recompose the matrix to perform their transformation.
To modify the matrix's transformation with an absolute parent frame of reference,
retrieve the settings with the decompose() method and make the appropriate
changes. You can then set the Matrix3D object to the modified transformation
using the recompose() method.
The decompose() method's parameter specifies the orientation style that is
meant to be used for the transformation. The default orientation is eulerAngles,
which defines the orientation with three separate angles of rotation for each
axis. The rotations occur consecutively and do not change the axis of each other.
The display object's axis rotation properties perform Euler Angles orientation
style transformation. The other orientation style options are axisAngle and
quaternion. The Axis Angle orientation uses a combination of an axis and an
angle to determine the orientation. The axis around which the object is rotated
is a unit vector that represents a direction. The angle represents the magnitude
of the rotation about the vector. The direction also determines where a display
object is facing and the angle determines which way is up. The appendRotation()
and prependRotation() methods use the Axis Angle orientation. The quaternion
orientation uses complex numbers and the fourth element of a vector. The three
axes of rotation (x,y,z) and an angle of rotation (w) represent the orientation.
The interpolate() method uses quaternion.
Parameters:
orientationStyle | An optional parameter that determines the orientation
style used for the matrix transformation. The three types of orientation style
are |
|---|---|
output | An optional vector of three Vector3D objects to be used and returned to avoid the runtime creating new objects. |
Returns:
A Vector of three Vector3D objects, each holding the translation, rotation, and scale settings, respectively.
deltaTransformVector(v:Vector3D):Vector3D
Uses the transformation matrix without its translation elements to transform a
Vector3D object from one space coordinate to another. The returned Vector3D
object holds the new coordinates after the rotation and scaling transformations
have been applied. If the deltaTransformVector() method applies a matrix that
only contains a translation transformation, the returned Vector3D is the same as
the original Vector3D object.
You can use the deltaTransformVector() method to have a display object in one
coordinate space respond to the rotation transformation of a second display
object. The object does not copy the rotation; it only changes its position to
reflect the changes in the rotation. For example, to use the display.Graphics
API for drawing a rotating 3D display object, you must map the object's rotating
coordinates to a 2D point. First, retrieve the object's 3D coordinates after each
rotation, using the deltaTransformVector() method. Next, apply the display
object's local3DToGlobal() method to translate the 3D coordinates to 2D points.
You can then use the 2D points to draw the rotating 3D object.
Note: This method automatically sets the w component of the passed Vector3D
to 0.0.
Parameters:
v | A Vector3D object holding the coordinates that are going to be transformed. |
|---|
Returns:
Vector3D A Vector3D object with the transformed coordinates.
deltaTransformVectorToOutput(v:Vector3D, output:Vector3D):Vector3D
Uses the transformation matrix without its translation elements to transform a
Vector3D object from one space coordinate to another. The returned Vector3D
object holds the new coordinates after the rotation and scaling transformations
have been applied. If the deltaTransformVector() method applies a matrix that
only contains a translation transformation, the returned Vector3D is the same as
the original Vector3D object.
You can use the deltaTransformVector() method to have a display object in one
coordinate space respond to the rotation transformation of a second display
object. The object does not copy the rotation; it only changes its position to
reflect the changes in the rotation. For example, to use the display.Graphics
API for drawing a rotating 3D display object, you must map the object's rotating
coordinates to a 2D point. First, retrieve the object's 3D coordinates after each
rotation, using the deltaTransformVector() method. Next, apply the display
object's local3DToGlobal() method to translate the 3D coordinates to 2D points.
You can then use the 2D points to draw the rotating 3D object.
Note: This method automatically sets the w component of the passed Vector3D
to 0.0.
Parameters:
v | A Vector3D object holding the coordinates that are going to be transformed. |
|---|---|
output | An optional Vector3D object to be used and returned to avoid the runtime creating a new object. |
Returns:
Vector3D A Vector3D object with the transformed coordinates.
identity():Void
Converts the current matrix to an identity or unit matrix. An identity matrix has
a value of one for the elements on the main diagonal and a value of zero for all
other elements. The result is a matrix where the rawData value is
1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1 and the rotation setting is set to
Vector3D(0,0,0), the position or translation setting is set to Vector3D(0,0,0),
and the scale is set to Vector3D(1,1,1). Here is a representation of an
identity matrix.
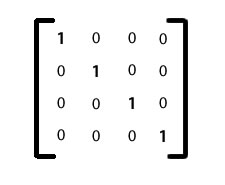
An object transformed by applying an identity matrix performs no transformation. In other words, if a matrix is multiplied by an identity matrix, the result is a matrix that is the same as (identical to) the original matrix.
interpolateTo(toMat:Matrix3D, percent:Float):Void
Interpolates this matrix towards the translation, rotation, and scale transformations of the target matrix.
The interpolateTo() method avoids the unwanted results that can occur when
using methods such as the display object's axis rotation properties. The
interpolateTo() method invalidates the cached value of the rotation property of
the display object and converts the orientation elements of the display object's
matrix to a quaternion before interpolation. This method guarantees the shortest,
most efficient path for the rotation. It also produces a smooth, gimbal-lock-free
rotation. A gimbal lock can occur when using Euler Angles, where each axis is
handled independently. During the rotation around two or more axes, the axes can
become aligned, leading to unexpected results. Quaternion rotation avoids the
gimbal lock.
Note: In case of interpolation, the scaling value of the matrix will reset and the matrix will be normalized.
Consecutive calls to the interpolateTo() method can produce the effect of a
display object starting quickly and then slowly approaching another display
object. For example, if the percent parameter is set to 0.1, the display object
moves ten percent toward the target object specified by the toMat parameter.
On subsequent calls or in subsequent frames, the object moves ten percent of the
remaining 90 percent, then ten percent of the remaining distance, and continues
until it reaches the target.
Parameters:
toMat | The target Matrix3D object. |
|---|---|
percent | A value between 0 and 1 that determines the location of the display object relative to the target. The closer the value is to 1.0, the closer the display object is to its current position. The closer the value is to 0, the closer the display object is to the target. |
invert():Bool
Inverts the current matrix. An inverted matrix is the same size as the original but performs the opposite transformation of the original matrix. For example, if the original matrix has an object rotate around the x axis in one direction, the inverse of the matrix will have the object rotate around the axis in the opposite direction. Applying an inverted matrix to an object undoes the transformation performed by the original matrix. If a matrix is multiplied by its inverse matrix, the result is an identity matrix.
An inverse of a matrix can be used to divide one matrix by another. The way to divide matrix A by matrix B is to multiply matrix A by the inverse of matrix B. The inverse matrix can also be used with a camera space. When the camera moves in the world space, the object in the world needs to move in the opposite direction to transform from the world view to the camera or view space. For example, if the camera moves closer, the objects becomes bigger. In other words, if the camera moves down the world z axis, the object moves up world z axis.
The invert() method replaces the current matrix with an inverted matrix. If you
want to invert a matrix without altering the current matrix, first copy the
current matrix by using the clone() method and then apply the invert() method
to the copy.
The Matrix3D object must be invertible.
Returns:
Returns true if the matrix was successfully inverted.
pointAt(pos:Vector3D, ?at:Vector3D, ?up:Vector3D):Void
Rotates the display object so that it faces a specified position. This method allows for an in-place modification to the orientation. The forward direction vector of the display object (the at Vector3D object) points at the specified world-relative position. The display object's up direction is specified with the up Vector3D object.
The pointAt() method invalidates the cached rotation property value of the
display object. The method decomposes the display object's matrix and modifies the
rotation elements to have the object turn to the specified position. It then
recomposes (updates) the display object's matrix, which performs the
transformation. If the object is pointing at a moving target, such as a moving
object's position, then with each subsequent call, the method has the object
rotate toward the moving target.
Note: If you use the Matrix3D.pointAt() method without setting the
optional parameters, a target object does not face the specified world-relative
position by default. You need to set the values for at to the -y-axis (0,-1,0)
and up to the -z axis (0,0,-1).
Parameters:
pos | The world-relative position of the target object. World-relative defines the object's transformation relative to the world space and coordinates, where all objects are positioned. |
|---|---|
at | The object-relative vector that defines where the display object is pointing. Object-relative defines the object's transformation relative to the object space, the object's own frame of reference and coordinate system. Default value is the +y axis (0,1,0). |
up | The object-relative vector that defines "up" for the display object. If the object is drawn looking down from above, the +z axis is its "up" vector. Object-relative defines the object's transformation relative to the object space, the object's own frame of reference and coordinate system. Default value is the +z-axis (0,0,1). |
prepend(rhs:Matrix3D):Void
Prepends a matrix by multiplying the current Matrix3D object by another Matrix3D object. The result combines both matrix transformations.
Matrix multiplication is different from matrix addition. Matrix multiplication is
not commutative. In other words, A times B is not equal to B times A. With the
prepend() method, the multiplication happens from the right side, meaning the rhs
Matrix3D object is on the right side of the multiplication operator.
thisMatrix = thisMatrix * rhsThe modifications made by prepend() method are object-space-relative. In other
words, they are always relative to the object's initial frame of reference.
The prepend() method replaces the current matrix with the prepended matrix. If
you want to prepend two matrixes without altering the current matrix, first copy
the current matrix by using the clone() method and then apply the prepend()
method to the copy.
Parameters:
rhs | A right-hand-side of the matrix by which the current Matrix3D is multiplied. |
|---|
prependRotation(degrees:Float, axis:Vector3D, ?pivotPoint:Vector3D):Void
Prepends an incremental rotation to a Matrix3D object. When the Matrix3D object is applied to a display object, the matrix performs the rotation before other transformations in the Matrix3D object.
The display object's rotation is defined by an axis, an incremental degree of
rotation around the axis, and an optional pivot point for the center of the
object's rotation. The axis can be any general direction. The common axes are the
X_AXIS (Vector3D(1,0,0)), Y_AXIS (Vector3D(0,1,0)), and
Z_AXIS (Vector3D(0,0,1)). In aviation terminology, the rotation about the y
axis is called yaw. The rotation about the x axis is called pitch. The rotation
about the z axis is called roll.
The order of transformation matters. A rotation followed by a translation transformation produces a different effect than a translation followed by a rotation.
The rotation effect is not absolute. The effect is object-relative, relative to
the frame of reference of the original position and orientation. To make an
absolute change to the transformation, use the recompose() method.
When the prependRotation() method's transformation is applied to a Matrix3D
object of a display object, the cached rotation property values of the display
object are invalidated.
One way to have a display object rotate around a specific point relative to its
location is to set the translation of the object to the specified point, rotate
the object using the prependRotation() method, and translate the object back to
the original position. In the following example, the myObject 3D display object
makes a y-axis rotation around the coordinate (10,10,0).
myObject.z = 1;
myObject.transform.matrix3D.prependTranslation(10,10,0);
myObject.transform.matrix3D.prependRotation(1, Vector3D.Y_AXIS);
myObject.transform.matrix3D.prependTranslation(-10,-10,0);Parameters:
degrees | The degree of rotation. |
|---|---|
axis | The axis or direction of rotation. The usual axes are the
|
pivotPoint | A point that determines the center of rotation. The default pivot point for an object is its registration point. |
prependScale(xScale:Float, yScale:Float, zScale:Float):Void
Prepends an incremental scale change along the x, y, and z axes to a Matrix3D object. When the Matrix3D object is applied to a display object, the matrix performs the scale changes before other transformations in the Matrix3D object. The changes are object-relative, relative to the frame of reference of the original position and orientation. The default scale factor is (1.0, 1.0, 1.0).
The scale is defined as a set of three incremental changes along the three axes (x,y,z). You can multiply each axis with a different number. When the scale changes are applied to a display object, the object's size increases or decreases. For example, setting the x, y, and z axes to two doubles the size of the object, while setting the axes to 0.5 halves the size. To make sure that the scale transformation only affects a specific axis, set the other parameters to one. A parameter of one means no scale change along the specific axis.
The prependScale() method can be used for resizing as well as for managing
distortions, such as stretch or contract of a display object. It can also be used
for zooming in and out on a location. Scale transformations are automatically
performed during a display object's rotation and translation.
The order of transformation matters. A resizing followed by a translation transformation produces a different effect than a translation followed by a resizing transformation.
Parameters:
xScale | A multiplier used to scale the object along the x axis. |
|---|---|
yScale | A multiplier used to scale the object along the y axis. |
zScale | A multiplier used to scale the object along the z axis. |
prependTranslation(x:Float, y:Float, z:Float):Void
Prepends an incremental translation, a repositioning along the x, y, and z axes, to a Matrix3D object. When the Matrix3D object is applied to a display object, the matrix performs the translation changes before other transformations in the Matrix3D object.
Translation specifies the distance the display object moves from its current
location along the x, y, and z axes. The prependTranslation() method sets the
translation as a set of three incremental changes along the three axes (x,y,z).
To have a translation change only a specific axis, set the other parameters to
zero. A zero parameter means no change along the specific axis.
The translation changes are not absolute. The effect is object-relative,
relative to the frame of reference of the original position and orientation.
To make an absolute change to the transformation matrix, use the recompose()
method. The order of transformation also matters. A translation followed by a
rotation transformation produces a different effect than a rotation followed by
a translation transformation. When prependTranslation() is used, the display
object continues to move in the direction it is facing, regardless of the other
transformations. For example, if a display object was facing toward a positive x
axis, it continues to move in the direction specified by the
prependTranslation() method, regardless of how the object has been rotated. To
make translation changes occur after other transformations, use the
appendTranslation() method.
Parameters:
x | An incremental translation along the x axis. |
|---|---|
y | An incremental translation along the y axis. |
z | An incremental translation along the z axis. |
recompose(components:Vector<Vector3D>, orientationStyle:Orientation3D = EULER_ANGLES):Bool
Sets the transformation matrix's translation, rotation, and scale settings. Unlike
the incremental changes made by the display object's rotation properties or
Matrix3D object's rotation methods, the changes made by recompose() method are
absolute changes. The recompose() method overwrites the matrix's transformation.
To modify the matrix's transformation with an absolute parent frame of reference,
retrieve the settings with the decompose() method and make the appropriate
changes. You can then set the Matrix3D object to the modified transformation
using the recompose() method.
The recompose() method's parameter specifies the orientation style that was
used for the transformation. The default orientation is eulerAngles, which defines
the orientation with three separate angles of rotation for each axis. The
rotations occur consecutively and do not change the axis of each other. The
display object's axis rotation properties perform Euler Angles orientation style
transformation. The other orientation style options are axisAngle and quaternion.
The Axis Angle orientation uses the combination of an axis and an angle to
determine the orientation. The axis around which the object is rotated is a unit
vector that represents a direction. The angle represents the magnitude of the
rotation about the vector. The direction also determines where a display object
is facing and the angle determines which way is up. The appendRotation() and
prependRotation() methods use the Axis Angle orientation. The quaternion
orientation uses complex numbers and the fourth element of a vector. An
orientation is represented by the three axes of rotation (x,y,z) and an angle of
rotation (w). The interpolate() method uses quaternion.
Parameters:
components | A Vector of three Vector3D objects that replace the Matrix3D object's translation, rotation, and scale elements. |
|---|---|
orientationStyle | An optional parameter that determines the orientation
style used for the matrix transformation. The three types of orientation styles
are eulerAngles (constant |
Returns:
Returns false if any of the Vector3D elements of the components
Vector do not exist or are null.
transformVector(v:Vector3D):Vector3D
Uses the transformation matrix to transform a Vector3D object from one space coordinate to another. The returned Vector3D object holds the new coordinates after the transformation. All the matrix transformations including translation are applied to the Vector3D object.
If the result of the transformVector() method was applied to the position of a
display object, only the display object's position changes. The display object's
rotation and scale elements remain the same.
Note: This method automatically sets the w component of the passed Vector3D to 1.0.
Parameters:
v | A Vector3D object holding the coordinates that are going to be transformed. |
|---|
Returns:
A Vector3D object with the transformed coordinates.
transformVectorToOutput(v:Vector3D, output:Vector3D):Vector3D
Uses the transformation matrix to transform a Vector3D object from one space coordinate to another. The returned Vector3D object holds the new coordinates after the transformation. All the matrix transformations including translation are applied to the Vector3D object.
If the result of the transformVector() method was applied to the position of a
display object, only the display object's position changes. The display object's
rotation and scale elements remain the same.
Note: This method automatically sets the w component of the passed Vector3D to 1.0.
Parameters:
v | A Vector3D object holding the coordinates that are going to be transformed. |
|---|---|
output | An optional Vector3D object to be used and returned to avoid the runtime creating a new object. |
Returns:
A Vector3D object with the transformed coordinates.
transformVectors(vin:Vector<Float>, vout:Vector<Float>):Void
Uses the transformation matrix to transform a Vector of Numbers from one
coordinate space to another. The tranformVectors() method reads every three
Numbers in the vin Vector object as a 3D coordinate (x,y,z) and places a
transformed 3D coordinate in the vout Vector object. All the matrix
transformations including translation are applied to the vin Vector object.
You can use the transformVectors() method to render and transform a 3D object
as a mesh. A mesh is a collection of vertices that defines the shape of the object.
Parameters:
vin | A Vector of Floats, where every three Numbers are a 3D coordinate (x,y,z) that is going to be transformed. |
|---|---|
vout | A Vector of Floats, where every three Numbers are a 3D transformed coordinate (x,y,z). |
transpose():Void
Converts the current Matrix3D object to a matrix where the rows and columns are
swapped. For example, if the current Matrix3D object's rawData contains the
following 16 numbers, 1,2,3,4,11,12,13,14,21,22,23,24,31,32,33,34, the
transpose() method reads every four elements as a row and turns the rows into
columns. The result is a matrix with the rawData of:
1,11,21,31,2,12,22,32,3,13,23,33,4,14,24,34.
The transpose() method replaces the current matrix with a transposed matrix.
If you want to transpose a matrix without altering the current matrix, first copy
the current matrix by using the clone() method and then apply the transpose()
method to the copy.
An orthogonal matrix is a square matrix whose transpose is equal to its inverse.