class PerspectiveMatrix3D

A Number that determines whether a matrix is invertible.

A Matrix3D object must be invertible. You can use the determinant property to make sure that a Matrix3D object is invertible. If determinant is zero, an inverse of the matrix does not exist. For example, if an entire row or column of a matrix is zero or if two rows or columns are equal, the determinant is zero. Determinant is also used to solve a series of equations.

Only a square matrix, like the Matrix3D class, has a determinant.

A Vector3D object that holds the position, the 3D coordinate (x,y,z) of a display object within the transformation's frame of reference. The position property provides immediate access to the translation vector of the display object's matrix without needing to decompose and recompose the matrix.

With the position property, you can get and set the translation elements of the transformation matrix.

A Vector of 16 Numbers, where every four elements is a column of a 4x4 matrix.

An exception is thrown if the rawData property is set to a matrix that is not invertible. The Matrix3D object must be invertible. If a non-invertible matrix is needed, create a subclass of the Matrix3D object.

A Vector of 16 Numbers, where every four elements is a column of a 4x4 matrix.

An exception is thrown if the rawData property is set to a matrix that is not invertible. The Matrix3D object must be invertible. If a non-invertible matrix is needed, create a subclass of the Matrix3D object.

Appends an incremental rotation to a Matrix3D object. When the Matrix3D object is applied to a display object, the matrix performs the rotation after other transformations in the Matrix3D object.

The display object's rotation is defined by an axis, an incremental degree of rotation around the axis, and an optional pivot point for the center of the object's rotation. The axis can be any general direction. The common axes are the X_AXIS (Vector3D(1,0,0)), Y_AXIS (Vector3D(0,1,0)), and Z_AXIS (Vector3D(0,0,1)). In aviation terminology, the rotation about the y axis is called yaw. The rotation about the x axis is called pitch. The rotation about the z axis is called roll.

The order of transformation matters. A rotation followed by a translation transformation produces a different effect than a translation followed by a rotation transformation.

The rotation effect is not absolute. It is relative to the current position and orientation. To make an absolute change to the transformation matrix, use the recompose() method. The appendRotation() method is also different from the axis rotation property of the display object, such as rotationX property. The rotation property is always performed before any translation, whereas the appendRotation() method is performed relative to what is already in the matrix. To make sure that you get a similar effect as the display object's axis rotation property, use the prependRotation() method, which performs the rotation before other transformations in the matrix.

When the appendRotation() method's transformation is applied to a Matrix3D object of a display object, the cached rotation property values of the display object are invalidated.

One way to have a display object rotate around a specific point relative to its location is to set the translation of the object to the specified point, rotate the object using the appendRotation() method, and translate the object back to the original position. In the following example, the myObject 3D display object makes a y-axis rotation around the coordinate (10,10,0).

myObject.z = 1;
myObject.transform.matrix3D.appendTranslation(10,10,0);
myObject.transform.matrix3D.appendRotation(1, Vector3D.Y_AXIS);
myObject.transform.matrix3D.appendTranslation(-10,-10,0);

Parameters:

Appends an incremental scale change along the x, y, and z axes to a Matrix3D object. When the Matrix3D object is applied to a display object, the matrix performs the scale changes after other transformations in the Matrix3D object. The default scale factor is (1.0, 1.0, 1.0).

The scale is defined as a set of three incremental changes along the three axes (x,y,z). You can multiply each axis with a different number. When the scale changes are applied to a display object, the object's size increases or decreases. For example, setting the x, y, and z axes to two doubles the size of the object, while setting the axes to 0.5 halves the size. To make sure that the scale transformation only affects a specific axis, set the other parameters to one. A parameter of one means no scale change along the specific axis.

The appendScale() method can be used for resizing as well as for managing distortions, such as stretch or contract of a display object, or for zooming in and out on a location. Scale transformations are automatically performed during a display object's rotation and translation.

The order of transformation matters. A resizing followed by a translation transformation produces a different effect than a translation followed by a resizing transformation.

Parameters:

Appends an incremental translation, a repositioning along the x, y, and z axes, to a Matrix3D object. When the Matrix3D object is applied to a display object, the matrix performs the translation changes after other transformations in the Matrix3D object.

The translation is defined as a set of three incremental changes along the three axes (x,y,z). When the transformation is applied to a display object, the display object moves from it current location along the x, y, and z axes as specified by the parameters. To make sure that the translation only affects a specific axis, set the other parameters to zero. A zero parameter means no change along the specific axis.

The translation changes are not absolute. They are relative to the current position and orientation of the matrix. To make an absolute change to the transformation matrix, use the recompose() method. The order of transformation also matters. A translation followed by a rotation transformation produces a different effect than a rotation followed by a translation.

Parameters:

Returns a new Matrix3D object that is an exact copy of the current Matrix3D object.

Returns:

Copies a Vector3D object into specific column of the calling Matrix3D object.

Parameters:

Copies specific column of the calling Matrix3D object into the Vector3D object.

Parameters:

Copies all of the matrix data from the source Matrix3D object into the calling Matrix3D object.

Parameters:

Copies all of the vector data from the source vector object into the calling Matrix3D object. The optional index parameter allows you to select any starting slot in the vector.

Parameters:

Copies all of the matrix data from the calling Matrix3D object into the provided vector. The optional index parameter allows you to select any target starting slot in the vector.

Parameters:

Copies a Vector3D object into specific row of the calling Matrix3D object.

Parameters:

Copies specific row of the calling Matrix3D object into the Vector3D object.

Parameters:

Parameters:

Returns the transformation matrix's translation, rotation, and scale settings as a Vector of three Vector3D objects. The first Vector3D object holds the translation elements. The second Vector3D object holds the rotation elements. The third Vector3D object holds the scale elements.

Some Matrix3D methods, such as the interpolateTo() method, automatically decompose and recompose the matrix to perform their transformation.

To modify the matrix's transformation with an absolute parent frame of reference, retrieve the settings with the decompose() method and make the appropriate changes. You can then set the Matrix3D object to the modified transformation using the recompose() method.

The decompose() method's parameter specifies the orientation style that is meant to be used for the transformation. The default orientation is eulerAngles, which defines the orientation with three separate angles of rotation for each axis. The rotations occur consecutively and do not change the axis of each other. The display object's axis rotation properties perform Euler Angles orientation style transformation. The other orientation style options are axisAngle and quaternion. The Axis Angle orientation uses a combination of an axis and an angle to determine the orientation. The axis around which the object is rotated is a unit vector that represents a direction. The angle represents the magnitude of the rotation about the vector. The direction also determines where a display object is facing and the angle determines which way is up. The appendRotation() and prependRotation() methods use the Axis Angle orientation. The quaternion orientation uses complex numbers and the fourth element of a vector. The three axes of rotation (x,y,z) and an angle of rotation (w) represent the orientation. The interpolate() method uses quaternion.

Parameters:

Returns:

Returns the transformation matrix's translation, rotation, and scale settings as a Vector of three Vector3D objects. The first Vector3D object holds the translation elements. The second Vector3D object holds the rotation elements. The third Vector3D object holds the scale elements.

Some Matrix3D methods, such as the interpolateTo() method, automatically decompose and recompose the matrix to perform their transformation.

To modify the matrix's transformation with an absolute parent frame of reference, retrieve the settings with the decompose() method and make the appropriate changes. You can then set the Matrix3D object to the modified transformation using the recompose() method.

The decompose() method's parameter specifies the orientation style that is meant to be used for the transformation. The default orientation is eulerAngles, which defines the orientation with three separate angles of rotation for each axis. The rotations occur consecutively and do not change the axis of each other. The display object's axis rotation properties perform Euler Angles orientation style transformation. The other orientation style options are axisAngle and quaternion. The Axis Angle orientation uses a combination of an axis and an angle to determine the orientation. The axis around which the object is rotated is a unit vector that represents a direction. The angle represents the magnitude of the rotation about the vector. The direction also determines where a display object is facing and the angle determines which way is up. The appendRotation() and prependRotation() methods use the Axis Angle orientation. The quaternion orientation uses complex numbers and the fourth element of a vector. The three axes of rotation (x,y,z) and an angle of rotation (w) represent the orientation. The interpolate() method uses quaternion.

Parameters:

Returns:

Uses the transformation matrix without its translation elements to transform a Vector3D object from one space coordinate to another. The returned Vector3D object holds the new coordinates after the rotation and scaling transformations have been applied. If the deltaTransformVector() method applies a matrix that only contains a translation transformation, the returned Vector3D is the same as the original Vector3D object.

You can use the deltaTransformVector() method to have a display object in one coordinate space respond to the rotation transformation of a second display object. The object does not copy the rotation; it only changes its position to reflect the changes in the rotation. For example, to use the display.Graphics API for drawing a rotating 3D display object, you must map the object's rotating coordinates to a 2D point. First, retrieve the object's 3D coordinates after each rotation, using the deltaTransformVector() method. Next, apply the display object's local3DToGlobal() method to translate the 3D coordinates to 2D points. You can then use the 2D points to draw the rotating 3D object.

Note: This method automatically sets the w component of the passed Vector3D to 0.0.

Parameters:

Returns:

Uses the transformation matrix without its translation elements to transform a Vector3D object from one space coordinate to another. The returned Vector3D object holds the new coordinates after the rotation and scaling transformations have been applied. If the deltaTransformVector() method applies a matrix that only contains a translation transformation, the returned Vector3D is the same as the original Vector3D object.

You can use the deltaTransformVector() method to have a display object in one coordinate space respond to the rotation transformation of a second display object. The object does not copy the rotation; it only changes its position to reflect the changes in the rotation. For example, to use the display.Graphics API for drawing a rotating 3D display object, you must map the object's rotating coordinates to a 2D point. First, retrieve the object's 3D coordinates after each rotation, using the deltaTransformVector() method. Next, apply the display object's local3DToGlobal() method to translate the 3D coordinates to 2D points. You can then use the 2D points to draw the rotating 3D object.

Note: This method automatically sets the w component of the passed Vector3D to 0.0.

Parameters:

Returns:

Converts the current matrix to an identity or unit matrix. An identity matrix has a value of one for the elements on the main diagonal and a value of zero for all other elements. The result is a matrix where the rawData value is 1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1 and the rotation setting is set to Vector3D(0,0,0), the position or translation setting is set to Vector3D(0,0,0), and the scale is set to Vector3D(1,1,1). Here is a representation of an identity matrix.

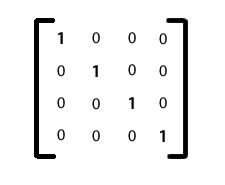
An object transformed by applying an identity matrix performs no transformation. In other words, if a matrix is multiplied by an identity matrix, the result is a matrix that is the same as (identical to) the original matrix.

Interpolates this matrix towards the translation, rotation, and scale transformations of the target matrix.

The interpolateTo() method avoids the unwanted results that can occur when using methods such as the display object's axis rotation properties. The interpolateTo() method invalidates the cached value of the rotation property of the display object and converts the orientation elements of the display object's matrix to a quaternion before interpolation. This method guarantees the shortest, most efficient path for the rotation. It also produces a smooth, gimbal-lock-free rotation. A gimbal lock can occur when using Euler Angles, where each axis is handled independently. During the rotation around two or more axes, the axes can become aligned, leading to unexpected results. Quaternion rotation avoids the gimbal lock.

Note: In case of interpolation, the scaling value of the matrix will reset and the matrix will be normalized.

Consecutive calls to the interpolateTo() method can produce the effect of a display object starting quickly and then slowly approaching another display object. For example, if the percent parameter is set to 0.1, the display object moves ten percent toward the target object specified by the toMat parameter. On subsequent calls or in subsequent frames, the object moves ten percent of the remaining 90 percent, then ten percent of the remaining distance, and continues until it reaches the target.

Parameters:

Inverts the current matrix. An inverted matrix is the same size as the original but performs the opposite transformation of the original matrix. For example, if the original matrix has an object rotate around the x axis in one direction, the inverse of the matrix will have the object rotate around the axis in the opposite direction. Applying an inverted matrix to an object undoes the transformation performed by the original matrix. If a matrix is multiplied by its inverse matrix, the result is an identity matrix.

An inverse of a matrix can be used to divide one matrix by another. The way to divide matrix A by matrix B is to multiply matrix A by the inverse of matrix B. The inverse matrix can also be used with a camera space. When the camera moves in the world space, the object in the world needs to move in the opposite direction to transform from the world view to the camera or view space. For example, if the camera moves closer, the objects becomes bigger. In other words, if the camera moves down the world z axis, the object moves up world z axis.

The invert() method replaces the current matrix with an inverted matrix. If you want to invert a matrix without altering the current matrix, first copy the current matrix by using the clone() method and then apply the invert() method to the copy.

The Matrix3D object must be invertible.

Returns:

Rotates the display object so that it faces a specified position. This method allows for an in-place modification to the orientation. The forward direction vector of the display object (the at Vector3D object) points at the specified world-relative position. The display object's up direction is specified with the up Vector3D object.

The pointAt() method invalidates the cached rotation property value of the display object. The method decomposes the display object's matrix and modifies the rotation elements to have the object turn to the specified position. It then recomposes (updates) the display object's matrix, which performs the transformation. If the object is pointing at a moving target, such as a moving object's position, then with each subsequent call, the method has the object rotate toward the moving target.

Note: If you use the Matrix3D.pointAt() method without setting the optional parameters, a target object does not face the specified world-relative position by default. You need to set the values for at to the -y-axis (0,-1,0) and up to the -z axis (0,0,-1).

Parameters:

Prepends a matrix by multiplying the current Matrix3D object by another Matrix3D object. The result combines both matrix transformations.

Matrix multiplication is different from matrix addition. Matrix multiplication is not commutative. In other words, A times B is not equal to B times A. With the prepend() method, the multiplication happens from the right side, meaning the rhs Matrix3D object is on the right side of the multiplication operator.

thisMatrix = thisMatrix * rhs

The modifications made by prepend() method are object-space-relative. In other words, they are always relative to the object's initial frame of reference.

The prepend() method replaces the current matrix with the prepended matrix. If you want to prepend two matrixes without altering the current matrix, first copy the current matrix by using the clone() method and then apply the prepend() method to the copy.

Parameters:

Prepends an incremental rotation to a Matrix3D object. When the Matrix3D object is applied to a display object, the matrix performs the rotation before other transformations in the Matrix3D object.

The display object's rotation is defined by an axis, an incremental degree of rotation around the axis, and an optional pivot point for the center of the object's rotation. The axis can be any general direction. The common axes are the X_AXIS (Vector3D(1,0,0)), Y_AXIS (Vector3D(0,1,0)), and Z_AXIS (Vector3D(0,0,1)). In aviation terminology, the rotation about the y axis is called yaw. The rotation about the x axis is called pitch. The rotation about the z axis is called roll.

The order of transformation matters. A rotation followed by a translation transformation produces a different effect than a translation followed by a rotation.

The rotation effect is not absolute. The effect is object-relative, relative to the frame of reference of the original position and orientation. To make an absolute change to the transformation, use the recompose() method.

When the prependRotation() method's transformation is applied to a Matrix3D object of a display object, the cached rotation property values of the display object are invalidated.

One way to have a display object rotate around a specific point relative to its location is to set the translation of the object to the specified point, rotate the object using the prependRotation() method, and translate the object back to the original position. In the following example, the myObject 3D display object makes a y-axis rotation around the coordinate (10,10,0).

myObject.z = 1;
myObject.transform.matrix3D.prependTranslation(10,10,0);
myObject.transform.matrix3D.prependRotation(1, Vector3D.Y_AXIS);
myObject.transform.matrix3D.prependTranslation(-10,-10,0);

Parameters:

Prepends an incremental scale change along the x, y, and z axes to a Matrix3D object. When the Matrix3D object is applied to a display object, the matrix performs the scale changes before other transformations in the Matrix3D object. The changes are object-relative, relative to the frame of reference of the original position and orientation. The default scale factor is (1.0, 1.0, 1.0).

The scale is defined as a set of three incremental changes along the three axes (x,y,z). You can multiply each axis with a different number. When the scale changes are applied to a display object, the object's size increases or decreases. For example, setting the x, y, and z axes to two doubles the size of the object, while setting the axes to 0.5 halves the size. To make sure that the scale transformation only affects a specific axis, set the other parameters to one. A parameter of one means no scale change along the specific axis.

The prependScale() method can be used for resizing as well as for managing distortions, such as stretch or contract of a display object. It can also be used for zooming in and out on a location. Scale transformations are automatically performed during a display object's rotation and translation.

The order of transformation matters. A resizing followed by a translation transformation produces a different effect than a translation followed by a resizing transformation.

Parameters:

Prepends an incremental translation, a repositioning along the x, y, and z axes, to a Matrix3D object. When the Matrix3D object is applied to a display object, the matrix performs the translation changes before other transformations in the Matrix3D object.

Translation specifies the distance the display object moves from its current location along the x, y, and z axes. The prependTranslation() method sets the translation as a set of three incremental changes along the three axes (x,y,z). To have a translation change only a specific axis, set the other parameters to zero. A zero parameter means no change along the specific axis.

The translation changes are not absolute. The effect is object-relative, relative to the frame of reference of the original position and orientation. To make an absolute change to the transformation matrix, use the recompose() method. The order of transformation also matters. A translation followed by a rotation transformation produces a different effect than a rotation followed by a translation transformation. When prependTranslation() is used, the display object continues to move in the direction it is facing, regardless of the other transformations. For example, if a display object was facing toward a positive x axis, it continues to move in the direction specified by the prependTranslation() method, regardless of how the object has been rotated. To make translation changes occur after other transformations, use the appendTranslation() method.

Parameters:

Sets the transformation matrix's translation, rotation, and scale settings. Unlike the incremental changes made by the display object's rotation properties or Matrix3D object's rotation methods, the changes made by recompose() method are absolute changes. The recompose() method overwrites the matrix's transformation.

To modify the matrix's transformation with an absolute parent frame of reference, retrieve the settings with the decompose() method and make the appropriate changes. You can then set the Matrix3D object to the modified transformation using the recompose() method.

The recompose() method's parameter specifies the orientation style that was used for the transformation. The default orientation is eulerAngles, which defines the orientation with three separate angles of rotation for each axis. The rotations occur consecutively and do not change the axis of each other. The display object's axis rotation properties perform Euler Angles orientation style transformation. The other orientation style options are axisAngle and quaternion. The Axis Angle orientation uses the combination of an axis and an angle to determine the orientation. The axis around which the object is rotated is a unit vector that represents a direction. The angle represents the magnitude of the rotation about the vector. The direction also determines where a display object is facing and the angle determines which way is up. The appendRotation() and prependRotation() methods use the Axis Angle orientation. The quaternion orientation uses complex numbers and the fourth element of a vector. An orientation is represented by the three axes of rotation (x,y,z) and an angle of rotation (w). The interpolate() method uses quaternion.

Parameters:

Returns:

Uses the transformation matrix to transform a Vector3D object from one space coordinate to another. The returned Vector3D object holds the new coordinates after the transformation. All the matrix transformations including translation are applied to the Vector3D object.

If the result of the transformVector() method was applied to the position of a display object, only the display object's position changes. The display object's rotation and scale elements remain the same.

Note: This method automatically sets the w component of the passed Vector3D to 1.0.

Parameters:

Returns:

Uses the transformation matrix to transform a Vector3D object from one space coordinate to another. The returned Vector3D object holds the new coordinates after the transformation. All the matrix transformations including translation are applied to the Vector3D object.

If the result of the transformVector() method was applied to the position of a display object, only the display object's position changes. The display object's rotation and scale elements remain the same.

Note: This method automatically sets the w component of the passed Vector3D to 1.0.

Parameters:

Returns:

Uses the transformation matrix to transform a Vector of Numbers from one coordinate space to another. The tranformVectors() method reads every three Numbers in the vin Vector object as a 3D coordinate (x,y,z) and places a transformed 3D coordinate in the vout Vector object. All the matrix transformations including translation are applied to the vin Vector object. You can use the transformVectors() method to render and transform a 3D object as a mesh. A mesh is a collection of vertices that defines the shape of the object.

Parameters:

Converts the current Matrix3D object to a matrix where the rows and columns are swapped. For example, if the current Matrix3D object's rawData contains the following 16 numbers, 1,2,3,4,11,12,13,14,21,22,23,24,31,32,33,34, the transpose() method reads every four elements as a row and turns the rows into columns. The result is a matrix with the rawData of: 1,11,21,31,2,12,22,32,3,13,23,33,4,14,24,34.

The transpose() method replaces the current matrix with a transposed matrix. If you want to transpose a matrix without altering the current matrix, first copy the current matrix by using the clone() method and then apply the transpose() method to the copy.

An orthogonal matrix is a square matrix whose transpose is equal to its inverse.